백준 9471 : 피사노 주기
문제 링크
9471번: 피사노 주기
첫째 줄에 테스트 케이스의 개수 P (1 ≤ P ≤ 1000)가 주어진다. 각 테스트 케이스는 N과 M으로 이루어져 있다. N은 테스트 케이스의 번호이고, M은 문제에서 설명한 m이다. (2 ≤ M ≤ 1,000,000)
www.acmicpc.net
문제 내용
1960년, IBM의 직원 Donald Wall은 피보나치수열을 m으로 나눈 나머지가 주기를 이룬다는 것을 증명했다.
예를 들어, 피보나치 수열의 처음 10개를 11로 나눈 예는 다음과 같다.
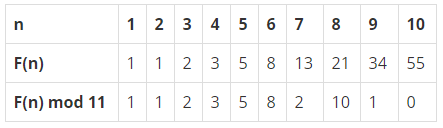
나머지를 이용해서 만든 수열은 주기가 나타날 수 있다. k(m)을 반복하는 부분 수열의 길이라고 했을 때, k(11) = 10 임을 알 수 있다.
Wall은 아래와 같은 여러 가지 성질도 증명했다.
- m > 2인 경우에 k(m)은 짝수이다.
- 임의의 짝수 정수 n > 2에 대해서, k(m) = n인 m이 항상 존재한다.
- k(m) ≤ m2 - 1
- k(2n) = 3×2(n-1)
- k(5n) = 4 ×5n
- k(2 ×5n) = 6n
- n > 2라면, k(10n) = 15 × 10(n-1)
m이 주어졌을 때, k(m)을 구하는 프로그램을 작성하시오.
Idea
문제는 뭔가 거창하긴 한데 결국은 주기를 구하는 문제로, 위에 있는 수식을 이용해서 푸는 것이 아닌 처음부터 하나하나 검사하여 주기를 갖는 부분을 찾는 문제이다.
아마 위의 식들은 m으로 나눈 나머지에 대해 주기가 반드시 존재한다는 사실을 알려주고자 한 것 같다.
아래 코드는 다음과 같이 짰다.
- a는 첫 항이고, b는 두 번째 항이다.
- 처음에 둘 다 1로 시작하므로 마지막 역시 a와 b가 1이 된다면 한 주기가 완성된 것이다.
- m으로 나눈 나머지에 대해서만 고려하면 되므로 a+b를 하고 항상 %m을 해준다.
Code
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#include <stdio.h>
int main() {
int P, N, M;
scanf("%d", &P);
int cnt, a, b;
for (int i = 0; i < P; i++) {
scanf("%d %d", &N, &M);
cnt = 0;
a = b = 1;
while (1) {
int tmp = (a + b) % M;
a = b;
b = tmp;
cnt++;
//주기를 찾으면 break
if (a==1 && b == 1) break;
}
printf("%d %d\n", N, cnt);
}
return 0;
}
|
cs |

'백준 Baekjoon' 카테고리의 다른 글
| [C언어] 백준 1874 : 스택 수열 (0) | 2020.10.18 |
|---|---|
| [C언어] 백준 2749 : 피보나치 수 3 (0) | 2020.10.10 |
| [C언어] 백준 11047 : 동전 0 (0) | 2020.09.29 |
| [C언어] 백준 16926 : 배열 돌리기 1 (0) | 2020.09.29 |
| [C++] 백준 2346 : 풍선 터뜨리기 (0) | 2020.09.25 |